Toward a Sparse Interpretable Audio Codec

Table of Contents

Introduction

Most widely-used modern audio codecs, such as Ogg Vorbis and MP3, as well as more recent "neural" codecs like Meta's Encodec or Descript's are based on block-coding; audio is divided into overlapping, fixed-size "frames" which are then compressed. While they produce excellent reproduction quality and can be used for downstream tasks such as text-to-audio, they do not produce an intuitive, directly-interpretable representation.

In this work, we introduce a proof-of-concept audio encoder that encodes audio as a sparse set of events and their times-of-occurrence. Rudimentary physics-based assumptions are used to model attack and the physical resonance of both the instrument being played and the room in which a performance occurs, hopefully encouraging a sparse, parsimonious, and easy-to-interpret representation.

We imagine a near-future audio codec where some types of musical composition could take place directly in the audio codec space. Text-to-audio is an excellent interface for non-musicians creating background music for movies, advertisements or social media content, but it is our view that experienced musicians and composers work in a "space" not fully captured by language and will prefer a much finer-grained representation that affords an effectively infinite range of possible sounds.

This work clearly does not replace current music generation models, but could serve as the underlying encoding on which generative models are trained. It is the authors' intuition that models trained on this rich, symbolic representation might have a much deeper "understanding" of the content they produce, given the point-cloud-like nature of the signal. Instead of predicting the next frame, the generative model would be predicting the relationships between "events". Long-term coherence in musical generation has always been a difficult problem, and we speculate that many models spend enormous shares of their capacity learning to reproduce physical resonance, rather than the human forces that drive them in interesting, musical directions.

Early speech results from the LJ-Speech dataset can be found here.

Previous Work

This work takes inspiration from symbolic approaches, such as MIDI, iterative decomposition methods like matching pursuit, and granular synthesis, which represents audio as a sparse set of "grains" or simple audio atoms.

Model

Encoder

The encoder iteratively removes energy from the input spectrogram, producing an event vector and one-hot/dirac impulse representing the time of occurrence. Other representations of time are possible, e.g., a scalar value of seconds, or a binary vector representing the frame number with log2(n_samples dimensionality.

Encoder Diagram

Decoder

The decoder uses the 32-dimensional event vector to choose an attack envelope, evolving resonance, and room impulse response to model the acoustic event, and then "schedules" it by convolving the event with the one-hot/direc impulse. Audio is not produced using typical upsampling convolutions, avoiding artifacts and producing more natural-sounding events.

Training Procedure

We train on the MusicNet dataset dataset) for ~76 hours, selecting random ~6 second audio segments sampled at 22050hz (mono) with a batch-size of 2. The model takes the following steps for 32 iterations on each training sample:

  1. The encoder analyzes the STFT spectrogram of the signal, producing a single 32-dimensional event vector and a one-hot vector representing time-of-occurrence
  2. The decoder produces "raw" audio samples of the acoustic event
  3. an STFT spectrogram of the acoustic event is produced and subtracted from the input spectrogram
  4. The encoder analyzes the residual and the process is repeated

The model is trained to maximize the amount of energy removed from the original signal at each step, and to minimize an adversarial loss, produced by a small, convolutional down-sampling discriminator which is trained in parallel, analyzing both the real and reproduced signals in the STFT spectrogram domain. Half of the generated events are masked/removed when analyzed by the discriminator, encouraging each event vector to stand on its own as a realistic event.

All training and model code can be found here.

Streaming Algorithm

When encoding, the entire ~6-second spectrogram is analyzed, but its second-half is masked when choosing the next event. In this way, the model can slide along overlapping sections of audio and encode segments of arbitrary durations.

Future Work

Better Perceptual Audio Losses

Recent experiments use a greedy, per-event loss which maximizes the energy removed from the signal at each step, as well as a learned, adversarial loss. Reconstruction quality will likely benefit from a more perceptually-aligned loss and a larger, more diverse dataset.

Model Size, Training Time and Dataset

Firstly, this model is relatively small, weighing in at ~14M parameters (~80 MB on disk) and has only been trained for around 76 hours, so it seems there is a lot of space to increase the model size, dataset size and training time to further improve. The reconstruction quality of the examples on this page is not amazing, certainly not good enough even for a lossy audio codec, but the structure the model extracts seems like it could be used for many interesting applications, and future work will improve perceptual audio quality.

Different Event Generator Variants

The decoder side of the model is very interesting, and all sorts of physical modelling-like approaches could yield better, more realistic, and sparser renderings of the audio.

For example, simple RNNs might serve as a natural alternative to the encoder used for the sound reproductions in this article.

Cite this Article

If you'd like to cite this article, you can use the following BibTeX block.

Streaming Algorithm for Arbitrary-Length Audio Segments

In this latest iteration of the work, we introduce a "streaming" algorithm so that we can decompose audio segments of arbitrary lengths.

Original (Streaming)

Reconstruction (Streaming)

Audio Examples

Example 1

Original Audio

Reconstruction

We mask the second half of the input audio to enable the streaming algorithm, so only the first half of the input audio is reproduced.

Event Scatterplot

Time is along the x-axis, and a 32D -> 1D projection of event vectors using t-SNE constitutes the distribution along the y-axis.
Colors are produced via a random projection from 32D -> 3D (RGB). Here it becomes clear that there are many redundant/overlapping events. Future work will stress more sparsity and less event overlap, hopefully increasing interpretability further.

Individual Event Intermediate Steps

Here, we choose an individual event at random and demonstrate the intermediate decoder steps, including the original energy "impulse", the choice of resonance, and finally, the choice of a room impulse response.

Energy Impulse

Energy Convolved with Chosen Resonances

Deformation/Interpolation Between Chosen Resonances Over Time

Signal Convolved with Room Impulse Response

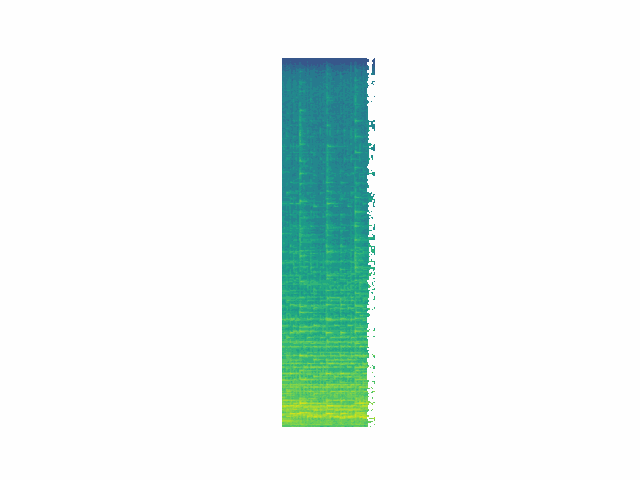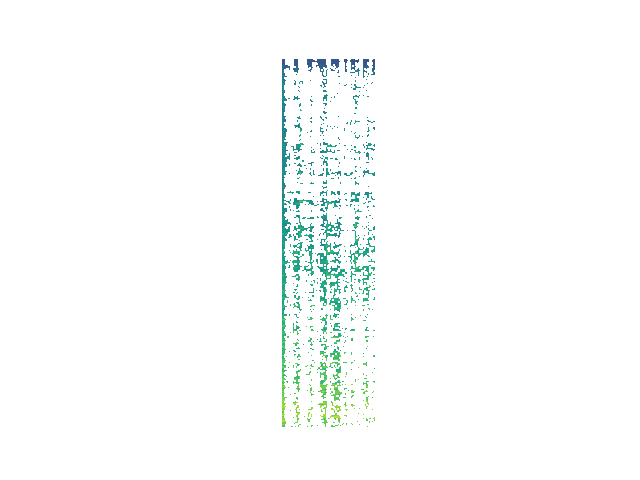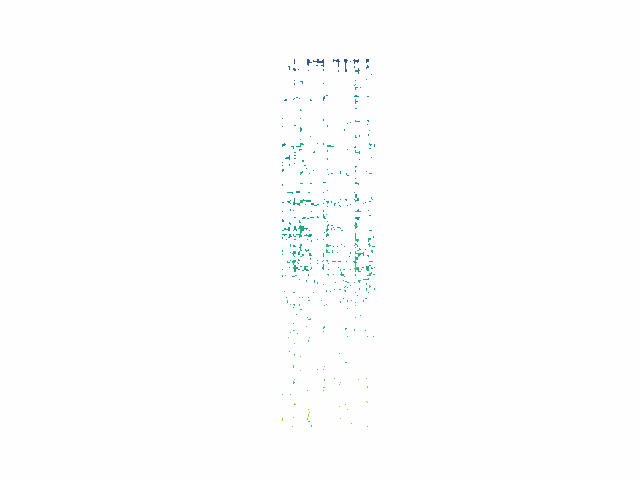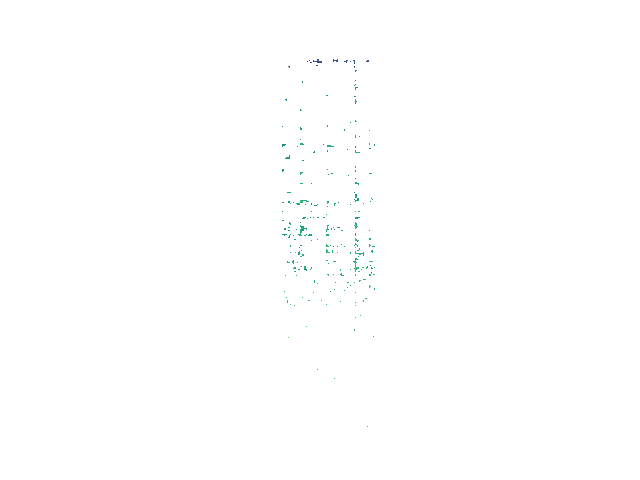
Decomposition Process

We can see that while energy is removed at each step, removed segments do not map cleanly onto audio "events" as a human listener would typically conceive of them. Future work will move toward fewer and more meaningul events via induced sparsity and/or clustering of events.

Randomized

Here, we generate random event vectors with the original event times.

Here we use the original event vectors, but choose random times.

Random Perturbations

Each event vector is "perturbed" or moved in the same direction in event space by adding a random event vector with small magnitude

Event Vectors

Different stopping conditions might be chosen during inference (e.g. norm of the residual) but during training, we remove energy for 32 steps.
Each event vector is of dimension 32. The decoder generates an event from this vector, which is then scheduled.

Example 2

Original Audio

Reconstruction

We mask the second half of the input audio to enable the streaming algorithm, so only the first half of the input audio is reproduced.

Event Scatterplot

Time is along the x-axis, and a 32D -> 1D projection of event vectors using t-SNE constitutes the distribution along the y-axis.
Colors are produced via a random projection from 32D -> 3D (RGB). Here it becomes clear that there are many redundant/overlapping events. Future work will stress more sparsity and less event overlap, hopefully increasing interpretability further.

Individual Event Intermediate Steps

Here, we choose an individual event at random and demonstrate the intermediate decoder steps, including the original energy "impulse", the choice of resonance, and finally, the choice of a room impulse response.

Energy Impulse

Energy Convolved with Chosen Resonances

Deformation/Interpolation Between Chosen Resonances Over Time

Signal Convolved with Room Impulse Response

Decomposition Process

We can see that while energy is removed at each step, removed segments do not map cleanly onto audio "events" as a human listener would typically conceive of them. Future work will move toward fewer and more meaningul events via induced sparsity and/or clustering of events.

Randomized

Here, we generate random event vectors with the original event times.

Here we use the original event vectors, but choose random times.

Random Perturbations

Each event vector is "perturbed" or moved in the same direction in event space by adding a random event vector with small magnitude

Event Vectors

Different stopping conditions might be chosen during inference (e.g. norm of the residual) but during training, we remove energy for 32 steps.
Each event vector is of dimension 32. The decoder generates an event from this vector, which is then scheduled.

Example 3

Original Audio

Reconstruction

We mask the second half of the input audio to enable the streaming algorithm, so only the first half of the input audio is reproduced.

Event Scatterplot

Time is along the x-axis, and a 32D -> 1D projection of event vectors using t-SNE constitutes the distribution along the y-axis.
Colors are produced via a random projection from 32D -> 3D (RGB). Here it becomes clear that there are many redundant/overlapping events. Future work will stress more sparsity and less event overlap, hopefully increasing interpretability further.

Individual Event Intermediate Steps

Here, we choose an individual event at random and demonstrate the intermediate decoder steps, including the original energy "impulse", the choice of resonance, and finally, the choice of a room impulse response.

Energy Impulse

Energy Convolved with Chosen Resonances

Deformation/Interpolation Between Chosen Resonances Over Time

Signal Convolved with Room Impulse Response

Decomposition Process

We can see that while energy is removed at each step, removed segments do not map cleanly onto audio "events" as a human listener would typically conceive of them. Future work will move toward fewer and more meaningul events via induced sparsity and/or clustering of events.

Randomized

Here, we generate random event vectors with the original event times.

Here we use the original event vectors, but choose random times.

Random Perturbations

Each event vector is "perturbed" or moved in the same direction in event space by adding a random event vector with small magnitude

Event Vectors

Different stopping conditions might be chosen during inference (e.g. norm of the residual) but during training, we remove energy for 32 steps.
Each event vector is of dimension 32. The decoder generates an event from this vector, which is then scheduled.

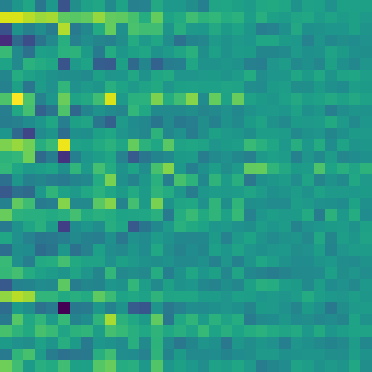
Example 4

Original Audio

Reconstruction

We mask the second half of the input audio to enable the streaming algorithm, so only the first half of the input audio is reproduced.

Event Scatterplot

Time is along the x-axis, and a 32D -> 1D projection of event vectors using t-SNE constitutes the distribution along the y-axis.
Colors are produced via a random projection from 32D -> 3D (RGB). Here it becomes clear that there are many redundant/overlapping events. Future work will stress more sparsity and less event overlap, hopefully increasing interpretability further.

Individual Event Intermediate Steps

Here, we choose an individual event at random and demonstrate the intermediate decoder steps, including the original energy "impulse", the choice of resonance, and finally, the choice of a room impulse response.

Energy Impulse

Energy Convolved with Chosen Resonances

Deformation/Interpolation Between Chosen Resonances Over Time

Signal Convolved with Room Impulse Response

Decomposition Process

We can see that while energy is removed at each step, removed segments do not map cleanly onto audio "events" as a human listener would typically conceive of them. Future work will move toward fewer and more meaningul events via induced sparsity and/or clustering of events.

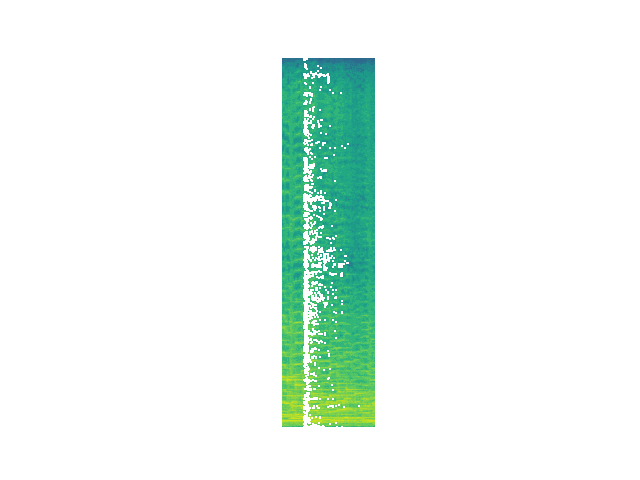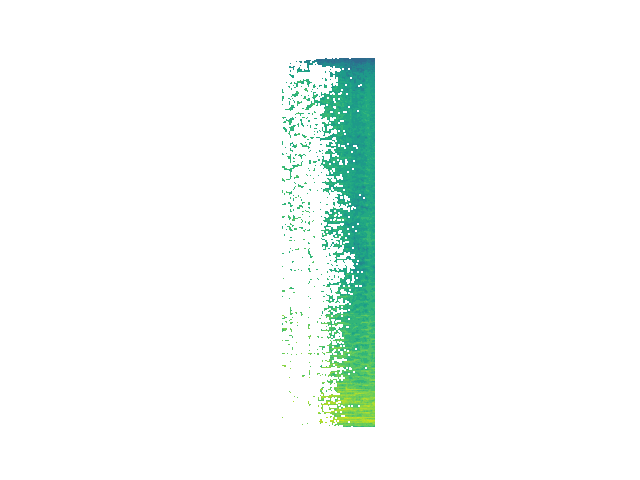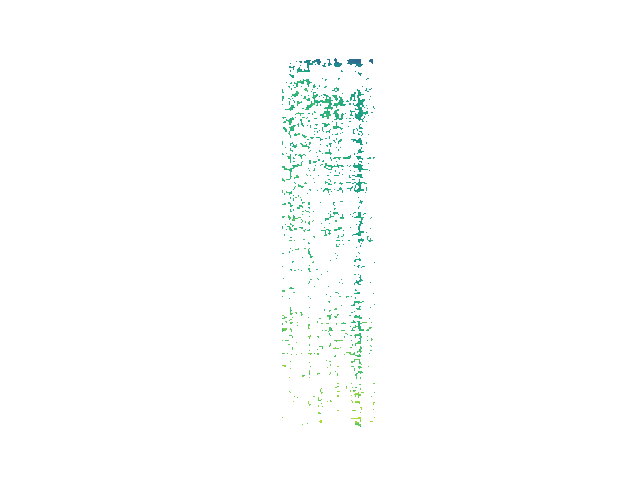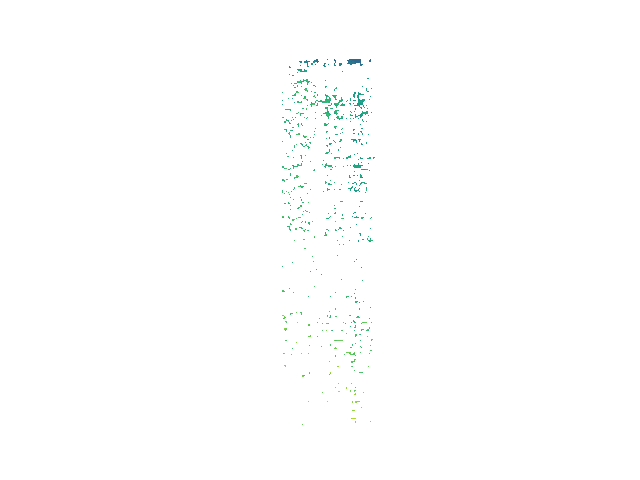
Randomized

Here, we generate random event vectors with the original event times.

Here we use the original event vectors, but choose random times.

Random Perturbations

Each event vector is "perturbed" or moved in the same direction in event space by adding a random event vector with small magnitude

Event Vectors

Different stopping conditions might be chosen during inference (e.g. norm of the residual) but during training, we remove energy for 32 steps.
Each event vector is of dimension 32. The decoder generates an event from this vector, which is then scheduled.

Example 5

Original Audio

Reconstruction

We mask the second half of the input audio to enable the streaming algorithm, so only the first half of the input audio is reproduced.

Event Scatterplot

Time is along the x-axis, and a 32D -> 1D projection of event vectors using t-SNE constitutes the distribution along the y-axis.
Colors are produced via a random projection from 32D -> 3D (RGB). Here it becomes clear that there are many redundant/overlapping events. Future work will stress more sparsity and less event overlap, hopefully increasing interpretability further.

Individual Event Intermediate Steps

Here, we choose an individual event at random and demonstrate the intermediate decoder steps, including the original energy "impulse", the choice of resonance, and finally, the choice of a room impulse response.

Energy Impulse

Energy Convolved with Chosen Resonances

Deformation/Interpolation Between Chosen Resonances Over Time

Signal Convolved with Room Impulse Response

Decomposition Process

We can see that while energy is removed at each step, removed segments do not map cleanly onto audio "events" as a human listener would typically conceive of them. Future work will move toward fewer and more meaningul events via induced sparsity and/or clustering of events.

Randomized

Here, we generate random event vectors with the original event times.

Here we use the original event vectors, but choose random times.

Random Perturbations

Each event vector is "perturbed" or moved in the same direction in event space by adding a random event vector with small magnitude

Event Vectors

Different stopping conditions might be chosen during inference (e.g. norm of the residual) but during training, we remove energy for 32 steps.
Each event vector is of dimension 32. The decoder generates an event from this vector, which is then scheduled.

n_samples = 2 ** 17 samples_per_event = 2048 # this is cut in half since we'll mask out the second half of encoder activations n_events = (n_samples // samples_per_event) // 2 context_dim = 32 # the samplerate, in hz, of the audio signal samplerate = 22050 # derived, the total number of seconds of audio n_seconds = n_samples / samplerate transform_window_size = 2048 transform_step_size = 256 n_frames = n_samples // transform_step_size from argparse import ArgumentParser from typing import Dict, Tuple, List import numpy as np import torch from sklearn.manifold import TSNE from torch import nn from conjure import S3Collection, \ conjure_article, CitationComponent, AudioComponent, ImageComponent, \ CompositeComponent, Logger, AudioTimelineComponent from data import get_one_audio_segment from iterativedecomposition import Model as IterativeDecompositionModel from modules.eventgenerators.overfitresonance import OverfitResonanceModel from modules import max_norm, sparse_softmax, amplitude_envelope import librosa remote_collection_name = 'iterative-decomposition-v4' def to_numpy(x: torch.Tensor): return x.data.cpu().numpy() # thanks to https://discuss.pytorch.org/t/how-do-i-check-the-number-of-parameters-of-a-model/4325/9 def count_parameters(model): return sum(p.numel() for p in model.parameters() if p.requires_grad) def process_events2( logger: Logger, events: torch.Tensor, vectors: torch.Tensor, times: torch.Tensor, total_seconds: float) -> Tuple[List[Dict], Dict]: # compute amplitude envelopes envelopes = amplitude_envelope(events, 128).data.cpu().numpy().reshape((n_events, -1)) # compute event positions/times, in seconds positions = torch.argmax(times, dim=-1, keepdim=True) / times.shape[-1] times = [float(x) for x in (positions * total_seconds).view(-1).data.cpu().numpy()] # normalize event vectors and map onto the y dimension normalized = vectors.data.cpu().numpy().reshape((-1, context_dim)) normalized = normalized - normalized.min(axis=0, keepdims=True) normalized = normalized / (normalized.max(axis=0, keepdims=True) + 1e-8) tsne = TSNE(n_components=1) points = tsne.fit_transform(normalized) points = points - points.min() points = points / (points.max() + 1e-8) print(points) # TODO: Use t-SNE for colors as well color_tsne = TSNE(n_components=3) colors = color_tsne.fit_transform(normalized) colors = colors - colors.min() colors = colors / (colors.max() + 1e-8) colors *= 255 colors = colors.astype(np.uint8) colors = [f'rgba({c[0]}, {c[1]}, {c[2]}, 0.5)' for c in colors] evts = {f'event{i}': events[:, i: i + 1, :] for i in range(events.shape[1])} event_components = {} scatterplot_srcs = [] for k, v in evts.items(): _, e = logger.log_sound(k, v) scatterplot_srcs.append(e.public_uri) event_components[k] = AudioComponent(e.public_uri, height=15, controls=False) return [{ 'eventTime': times[i], 'offset': times[i], 'y': float(points[i]), 'color': colors[i], 'audioUrl': scatterplot_srcs[i].geturl(), 'eventEnvelope': envelopes[i].tolist(), 'eventDuration': total_seconds, } for i in range(n_events)], event_components def load_model(wavetable_device: str = 'cpu') -> nn.Module: hidden_channels = 512 model = IterativeDecompositionModel( in_channels=1025, hidden_channels=hidden_channels, with_activation_norm=True, resonance_model=OverfitResonanceModel( n_noise_filters=64, noise_expressivity=2, noise_filter_samples=128, noise_deformations=32, instr_expressivity=4, n_events=1, n_resonances=4096, n_envelopes=256, n_decays=64, n_deformations=256, n_samples=n_samples, n_frames=n_frames, samplerate=samplerate, hidden_channels=hidden_channels, wavetable_device=wavetable_device, fine_positioning=True, fft_resonance=True, context_dim=context_dim )) with open('iterativedecomposition18.dat', 'rb') as f: model.load_state_dict(torch.load(f, map_location=lambda storage, loc: storage)) print('Total parameters', count_parameters(model)) print('Encoder parameters', count_parameters(model.encoder)) print('Decoder parameters', count_parameters(model.resonance)) return model def generate_multiple_events( model: nn.Module, vectors: torch.Tensor, times: torch.Tensor) -> torch.Tensor: generation_result = torch.cat( [model.generate(vectors[:, i:i + 1, :], times[:, i:i + 1, :]) for i in range(n_events)], dim=1) generation_result = torch.sum(generation_result, dim=1, keepdim=True) generation_result = max_norm(generation_result) return generation_result def generate( model: nn.Module, vectors: torch.Tensor, times: torch.Tensor, randomize_events: bool, randomize_times: bool) -> torch.Tensor: batch, n_events, _ = vectors.shape if randomize_events: vectors = torch.zeros_like(vectors).uniform_(vectors.min().item(), vectors.max().item()) if randomize_times: times = torch.zeros_like(times).uniform_(-1, 1) times = sparse_softmax(times, dim=-1, normalize=True) * times generation_result = generate_multiple_events(model, vectors, times) return generation_result def streaming_section(logger: Logger) -> CompositeComponent: model = load_model() samples = get_one_audio_segment(n_samples * 4, samplerate, device='cpu').view(1, 1, -1) with torch.no_grad(): recon = model.streaming(samples) recon = max_norm(recon) _, orig = logger.log_sound(key='streamingorig', audio=samples) orig = AudioComponent(orig.public_uri, height=100, controls=True, scale=4) _, recon = logger.log_sound(key='streamingrecon', audio=recon) recon = AudioComponent(recon.public_uri, height=100, controls=True, scale=4) return CompositeComponent( orig=orig, recon=recon, ) def make_audio_component( logger: Logger, samples: torch.Tensor, key: str, audio_color: str = 'rgba(100, 200, 150, 0.5)') -> AudioComponent: _, meta = logger.log_sound(key=key, audio=samples) audio_component = AudioComponent(meta.public_uri, height=100, color=audio_color) return audio_component def make_matrix_component( logger: Logger, samples: torch.Tensor, key: str, cmap: str = 'hot', height: int = 100) -> ImageComponent: try: _, meta = logger.log_matrix_with_cmap(key, samples[0, 0, :, :], cmap=cmap) except IndexError: _, meta = logger.log_matrix_with_cmap(key, samples, cmap=cmap) component = ImageComponent(meta.public_uri, height=height) return component def reconstruction_section(logger: Logger, example_number: int) -> CompositeComponent: model = load_model() # get a random audio segment samples = get_one_audio_segment(n_samples, samplerate, device='cpu').view(1, 1, n_samples) events, vectors, times, residuals = model.iterative(samples, return_all_residuals=True) # event_norms = torch.norm(events, dim=-1).view(-1) # logger.log # choose one of the earliest/most prominent events random_event_index = np.random.randint(0, n_events) _, intermediates = model.generate( vectors[:, random_event_index:random_event_index + 1, :], times[:, random_event_index:random_event_index + 1, :], include_intermediates = True) impulse_audio_component = make_audio_component(logger, max_norm(intermediates['impulse']), 'impulse') resonance_audio_component = make_audio_component(logger, max_norm(intermediates['dry']), 'dry') reverb_audio_component = make_audio_component(logger, max_norm(intermediates['wet']), 'wet') # TODO: These three lines are an incredibly common pattern, they should be at most 2 n_bins = 84 impulse_spec = librosa.cqt(intermediates['impulse'].data.cpu().numpy().reshape((-1,)), n_bins=n_bins) impulse_spec = impulse_spec[:, :128] impulse_spec = make_matrix_component( logger, np.log(1 + np.flipud(np.abs(impulse_spec))), 'impulsespec', height=200, cmap='gray') resonance_spec = librosa.cqt(intermediates['dry'].data.cpu().numpy().reshape((-1,)), n_bins=n_bins) resonance_spec = resonance_spec[:, :128] resonance_spec = make_matrix_component( logger, np.log(1 + np.flipud(np.abs(resonance_spec))), 'resonancespec', height=200, cmap='gray') reverb_spec = librosa.cqt(intermediates['wet'].data.cpu().numpy().reshape((-1,)), n_bins=n_bins) reverb_spec = reverb_spec[:, :128] reverb_spec = make_matrix_component( logger, np.log(1 + np.flipud(np.abs(reverb_spec))), 'reverbspec', height=200, cmap='gray') deformations = make_matrix_component( logger, max_norm(intermediates['deformations']), 'deformations', height=200) residuals = residuals.view(n_events, 1025, -1).data.cpu().numpy() residuals = residuals[:, ::-1, :] residuals = np.log(residuals + 1e-6) t = residuals.shape[-1] residuals = residuals[..., :t // 2] perturbation = torch.zeros(1, n_events, context_dim).uniform_(-10, 10) perturbed_vectors = vectors + perturbation # envelopes = amplitude_envelope(events, n_frames=64).data.cpu().numpy() _, movie = logger.log_movie('decomposition', residuals, fps=2) movie = ImageComponent(movie.public_uri, height=200, title='decomposition') audio_color = 'rgba(100, 200, 150, 0.5)' # generate audio with the same times, but randomized event vectors randomized_events = generate(model, vectors, times, randomize_events=True, randomize_times=False) _, random_events = logger.log_sound('randomizedevents', randomized_events) random_events_component = AudioComponent( random_events.public_uri, height=100, controls=True, color=audio_color) # generate audio with the same events, but randomized times randomized_times = generate(model, vectors, times, randomize_events=False, randomize_times=True) _, random_times = logger.log_sound('randomizedtimes', randomized_times) random_times_component = AudioComponent( random_times.public_uri, height=100, controls=True, color=audio_color) # generate audio with the same perturbation for all events perturbed = generate(model, perturbed_vectors, times, randomize_events=False, randomize_times=False) _, prt = logger.log_sound('perturbed', perturbed) perturbed_component = AudioComponent( prt.public_uri, height=100, controls=True, color=audio_color) total_seconds = n_samples / samplerate # points, times, colors = process_events(vectors, times, total_seconds) scatterplot_events, _ = process_events2(logger, events, vectors, times, total_seconds) # sum together all events summed = torch.sum(events, dim=1, keepdim=True) summed = max_norm(summed) # _, original = logger.log_sound(f'original', samples) # _, reconstruction = logger.log_sound(f'reconstruction', summed) original_spec = librosa.cqt(samples.data.cpu().numpy().reshape((-1,)), n_bins=n_bins) _, original_spec = logger.log_matrix_with_cmap('origspec', np.flipud(np.abs(original_spec)), cmap='hot') original_spec = ImageComponent(original_spec.public_uri, height=200, title='Original') recon_spec = librosa.cqt(summed.data.cpu().numpy().reshape((-1,)), n_bins=n_bins) _, recon_spec = logger.log_matrix_with_cmap('reconspec', np.flipud(np.abs(recon_spec)), cmap='hot') recon_spec = ImageComponent(recon_spec.public_uri, height=200, title='Reconstruction') # audio_color = 'rgba(100, 200, 150, 0.5)' # orig_audio_component = AudioComponent(original.public_uri, height=100, color=audio_color) # recon_audio_component = AudioComponent(reconstruction.public_uri, height=100, color=audio_color)orig_audio_component orig_audio_component = make_audio_component(logger, samples, 'original') recon_audio_component = make_audio_component(logger, summed, 'recon') scatterplot_component = AudioTimelineComponent( duration=total_seconds, width=600, height=300, events=scatterplot_events ) _, event_vectors = logger.log_matrix_with_cmap('latents', vectors[0].T, cmap='viridis') latents = ImageComponent(event_vectors.public_uri, height=200, title='latent event vectors', full_width=False) composite = CompositeComponent( header=f'## Example {example_number}', orig_header='### Original Audio', orig_audio=orig_audio_component, orig_spec=original_spec, recon_header='### Reconstruction', recon_content='''We mask the second half of the input audio to enable the streaming algorithm, so only the first half of the input audio is reproduced.''', recon_audio=recon_audio_component, recon_spec=recon_spec, scatterplot_header='''### Event Scatterplot''', scatterplot_content='''Time is along the x-axis, and a 32D -> 1D projection of event vectors using t-SNE constitutes the distribution along the y-axis. Colors are produced via a random projection from 32D -> 3D (RGB). Here it becomes clear that there are many redundant/overlapping events. Future work will stress more sparsity and less event overlap, hopefully increasing interpretability further. ''', scatterplot=scatterplot_component, intermediates_header='''### Individual Event Intermediate Steps''', intermediate_content='''Here, we choose an individual event at random and demonstrate the intermediate decoder steps, including the original energy "impulse", the choice of resonance, and finally, the choice of a room impulse response. ''', impulse_header='''#### Energy Impulse''', impulse=impulse_audio_component, impulse_spec=impulse_spec, resonance_header='''#### Energy Convolved with Chosen Resonances''', resonance=resonance_audio_component, resonance_spec=resonance_spec, deformation_header='''#### Deformation/Interpolation Between Chosen Resonances Over Time''', deformations=deformations, verb_header='''#### Signal Convolved with Room Impulse Response''', wet=reverb_audio_component, reverb_spec=reverb_spec, decomposition_header='''### Decomposition Process''', decomposition_content='''We can see that while energy is removed at each step, removed segments do not map cleanly onto audio "events" as a human listener would typically conceive of them. Future work will move toward fewer and more meaningul events via induced sparsity and/or clustering of events. ''', decomposition=movie, randomized_header='### Randomized', random_events_content='''Here, we generate random event vectors with the original event times. ''', random_events=random_events_component, random_times_content='''Here we use the original event vectors, but choose random times. ''', random_times=random_times_component, perturbed_header='### Random Perturbations', perturbed_content='''Each event vector is "perturbed" or moved in the same direction in event space by adding a random event vector with small magnitude ''', perturbed=perturbed_component, latents_header='''### Event Vectors''', latents_content='''Different stopping conditions might be chosen during inference (e.g. norm of the residual) but during training, we remove energy for 32 steps. Each event vector is of dimension 32. The decoder generates an event from this vector, which is then scheduled. ''', latents=latents, ) return composite

Notes

This blog post is generated from a Python script using conjure.

def demo_page_dict() -> Dict[str, any]: print(f'Generating article...') remote = S3Collection( remote_collection_name, is_public=True, cors_enabled=True) logger = Logger(remote) # print('Creating large scatterplot') # large_scatterplot = scatterplot_section(logger) print('Creating streaming section') streaming = streaming_section(logger) print('Creating reconstruction examples') example_1 = reconstruction_section(logger, 1) example_2 = reconstruction_section(logger, 2) example_3 = reconstruction_section(logger, 3) example_4 = reconstruction_section(logger, 4) example_5 = reconstruction_section(logger, 5) citation = CitationComponent( tag='johnvinyarditerativedecompositionv3', author='Vinyard, John', url='https://blog.cochlea.xyz/sparse-interpretable-audio-codec-paper.html', header='Toward a Sparse Interpretable Audio Codec', year='2025', ) return dict( streaming=streaming, example_1=example_1, example_2=example_2, example_3=example_3, example_4=example_4, example_5=example_5, citation=citation ) def generate_demo_page(): display = demo_page_dict() conjure_article( __file__, 'html', title='Toward a Sparse Interpretable Audio Codec', web_components_version='0.0.78', **display) if __name__ == '__main__': parser = ArgumentParser() parser.add_argument('--clear', action='store_true') parser.add_argument('--list', action='store_true') args = parser.parse_args() if args.list: remote = S3Collection( remote_collection_name, is_public=True, cors_enabled=True) print(remote) print('Listing stored keys') for key in remote.iter_prefix(start_key=b'', prefix=b''): print(key) if args.clear: remote = S3Collection( remote_collection_name, is_public=True, cors_enabled=True) remote.destroy(prefix=b'') generate_demo_page()
Back to Top